Nonlinear Controller Simulator Tester
| Links: Link

This project focuses on completing the Monza arcade game, a highly nonlinear system, by controlling the actuator that rotates the circuit by a given angle, . The goal is to navigate a coin through a maze without it falling off the track. The project involves deriving the equations of motion, identifying model parameters, and implementing different control strategies. A complete model of the Monza game was developed from scratch using Pygame library. The model includes a user interface for manual play or testing the controllers on different difficulty levels.
The game features four levels of difficulty, based on rail layout, with the objective to rotate the circuit to guide the coin to the final destination. The maze is modeled as eight parabolas, each with the same equation but vertically offset. Here is a demonstration of the developed simulator:
Dynamics of the System
The coin’s motion along the parabolic rails is influenced by several forces: gravity, friction, and air resistance. The improved model incorporates additional dynamics, such as friction between the coin and the rail, rolling resistance, and the effects of the board’s inclination. Equations for both sliding and rolling motion were derived to simulate the realistic behavior of the coin as it moves, falls to lower rails, and rebounds after impacts.
Control Strategies
Three control approaches were developed to manage the nonlinear dynamics of the Monza game:
Sliding Mode Control (SMC): This nonlinear control method drives the system to a predefined sliding surface in state space. The controller was tuned to minimize the error between the coin’s position and the target, adapting to different difficulty levels through trial and error.
Fuzzy Logic Control: A fuzzy logic controller was implemented to manage uncertainty and nonlinearity. Fuzzy sets for distance, speed, and angle were defined, with rules to govern how the board should rotate based on the coin’s position and speed. This approach allowed for intuitive, human-readable control logic.
Reinforcement Learning (RL): A Deep Q-Network (DQN) model was trained to control the board by learning through trial and error. The model received feedback based on the coin’s speed and position, and through training, it learned to optimize its actions to navigate the maze. Several neural network architectures and reward systems were tested to achieve the final working model.
Results and Future Work
The table below shows the completion times for each control method across the four difficulty levels:
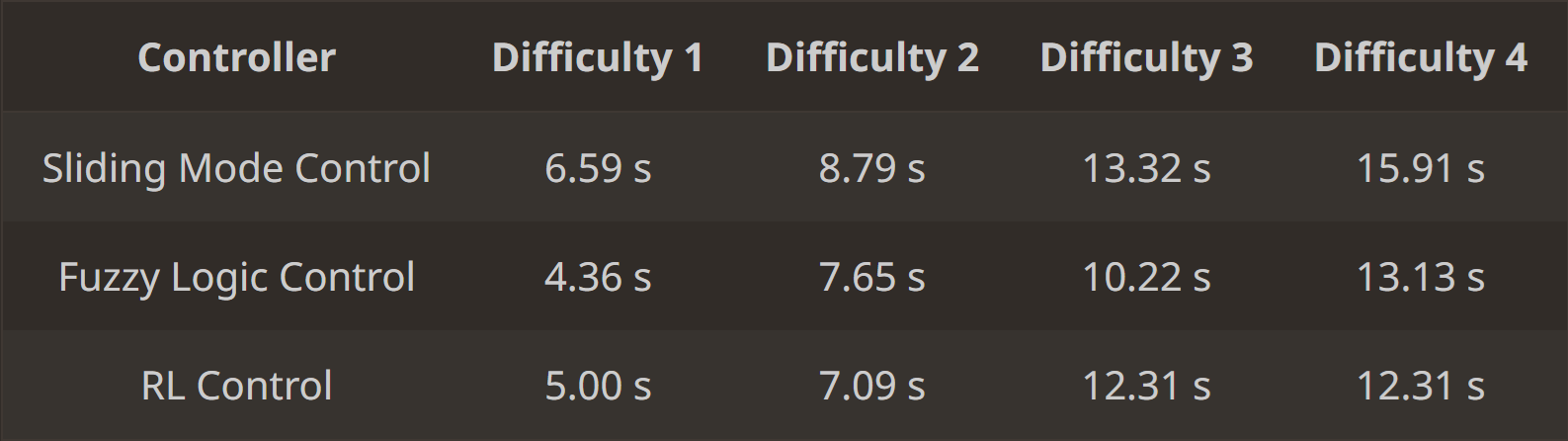
The fuzzy logic and RL controllers outperformed the Sliding Mode Control in terms of speed, as they took more aggressive actions. However, none of the controllers imposed physical constraints on angular acceleration, which would be necessary for real-world application. Future work would involve testing these controllers on a real Monza platform and refining the model to include angular acceleration constraints and the application of torque.
